Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
Filter By
Clear Filter

All Questions

The sum of $\overline{2} .75$ and $\overline{3} .78$ is :

Option: 1

$\overline{5} .53$


Option: 2

$\overline{4} .53$


Option: 3

$\overline{1} .53$


Option: 4

$\overline{1} .03$


B

View Full Answer(2)
Posted by

Karina kishor kadam

The simplification of $(0 . \overline{6}+0 . \overline{7}+0 . \overline{8}+0 . \overline{3})$ yields the result:

Option: 1

$10 / 9$


Option: 2

$20 / 9$


Option: 3

2. $\overline{35}$


Option: 4

$23 / 5$


B

 

View Full Answer(2)
Posted by

Karina kishor kadam

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

If a, b, c, d are inputs to a gate and x is its output, then, as per the following time graph, the gate is :
Option: 1 NOT
Option: 2 AND
Option: 3 OR
Option: 4 NAND
\

The output of OR gate is 0 when all inputs are 0 and output is 1 when at least one of the input is 1.

Observing output x it is 0 when all inputs are 0 and it is 1 when at least one of the inputs is 1
therefore, the gate is OR

View Full Answer(1)
Posted by

Ritika Jonwal

The amplitude of upper and lower side bands of A.M. wave where a carrier signal with frequency 11.21 \mathrm{MHz}, peak voltage 15 \mathrm{~V} is amplitude modulated by a 7.7 \mathrm{kHz} sine wave of 5 \mathrm{~V} amplitude are \frac{\mathrm{a}}{10} \mathrm{~V}$ and $\frac{\mathrm{b}}{10} \mathrm{~V} respectively. Then the value of \frac{a}{b} is______
 

\begin{gathered} f_{c}=11.21 \times 10^{6} \mathrm{~Hz} \\ A_{c}=15 \\ f_{m}=7.7 \times 10^{3} \mathrm{~Hz} \\ A_{m}=5 \mathrm{~V} \end{gathered}

\begin{aligned} \frac{a}{10}=\frac{b}{10} &=\frac{\mu A_{c}}{2} \\ \frac{a}{b} &=1 \end{aligned}

View Full Answer(1)
Posted by

vishal kumar

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

The maximum amplitude for an amplitude modulated wave is found to be 12V while the minimum amplitude is found to be 3V. The modulation index is 0.6x where x is ______.
 

\begin{aligned} &\text { Maximum \: amplitude}=V_{\text {max }}=12\\ \end{aligned}

\begin{aligned} &\text { Minimum amplitude }=V_{\text {min }}=3\\ \end{aligned}

\begin{aligned} &\mu =\frac{V_{\max }-V_{\min }}{V_{\max }+V_{\min }}=\frac{9}{15}\\ &\mu =0.6\\ &\therefore x=1 \end{aligned}

View Full Answer(1)
Posted by

vishal kumar

An amplitude modulated wave is represented by  C_{m}\left ( t \right )= 10\left ( 1+0\cdot 2\cos 12560t \right )\sin \left ( 111\times 10^{4}t \right ) volts. The modulating frequency in kHz will be -----------------------.
 

C_{m}\left ( t \right )= 10\left ( 1+0\cdot 2\cos 12560t \right )\sin \left ( 111\times 10^{4}t \right )
\omega _{m}= 12560= 2\pi f
12560= 6\cdot 28\times f
f= \frac{12560}{6\cdot 28}
= 2\cdot 0\, kHz
f= 2\, kHz 

View Full Answer(1)
Posted by

vishal kumar

NEET 2024 Most scoring concepts

    Just Study 32% of the NEET syllabus and Score up to 100% marks

A transmitting antenna at top of a tower has a height of 50 m and the height of receiving antenna is 80 m. What is the range of communication for Line of Sight (LoS) mode?
[use radius of earth = 6400 km]
Option: 1 80.2 km
Option: 2 144.1 km
Option: 3 57.28 km
Option: 4 45.5 km

Range\; of\: communication = \sqrt{2h_{T}R}+\sqrt{2h_{R}R}
                                                         = \sqrt{2\times 50\times 6400\times 10^{3}}+\sqrt{2\times 80\times 6400\times 10^{3}}
=10\times 80\times 10\sqrt{10}+40\times 80\times 10
=800\left ( 10\sqrt{10}+40 \right )
=800\left ( 31\cdot 62+40 \right )
Range=57\cdot 28\times 10^{3}m= 57\cdot 28\, km
The correct option is (3)

View Full Answer(1)
Posted by

vishal kumar

A transmitting antenna has a height of 320 \mathrm{~m} and that of receiving antenna is 2000 \mathrm{~m}. The maximum distance between them for satisfactory communication in line of sight mode is 'd'. The value of ' d ' is ________\mathrm{km}.
 

Range\, of\, communication= \sqrt{2h_{T}R}+\sqrt{2h_{R}R}
                                                        = \sqrt{2\times 320\times 6400\times 10^{3}}+\sqrt{2\times 2000\times 6400\times 10^{3}}
=80\times 80\times 10+200\times 80\times 10
=64000+160000
=224000 \, m
=224 \, km

View Full Answer(1)
Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

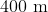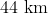An antenna is mounted on a 400 \mathrm{~m} tall building. What will be the wavelength of signal that can be radiated effectively by the transmission tower upto a range of 44 \mathrm{~km} ?
Option: 1 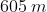605\: m
Option: 2 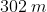302\: m
Option: 3 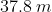37.8\: m
Option: 4 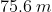75.6\: m

Range of Transmission = \sqrt{2hR}

Height of transmission tower = h= h_{building }+h_{antenna}

44000= \sqrt{2\times h\times 6400\times10^{3}}

44000\times 44000= 2h\times 6400\times10^{3}

h_{min}= 151.25

\lambda = 4h= 605m

View Full Answer(1)
Posted by

vishal kumar

If the sum of the heights of transmitting and receiving antennas in the line of sight of communication is fixed at 160 \mathrm{~m}, then the maximum range of LOS communication is___________\mathrm{km}.
(Take \: radius\: of \: Earth =6400 \mathrm{~km} ) 

Range of LOS communication = \sqrt{2h_{T}R}+\sqrt{2h_{R}R}
                 h_{T}+h_{R}=160\, m
For maximum range ,
h_{T}=h_{R}
\therefore h_{T}=h_{R}= 80 m
    = 2\sqrt{2h_{T}R}
    = 2\times \sqrt{2\times 80\times 6400\times 10^{3}}
    = 2\times \sqrt{160\times 6400\times 10^{3}}
   = 2\times80\times 40\times 10
\Rightarrow Range= 64000 m= 64\, km 

View Full Answer(1)
Posted by

vishal kumar

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE
filter_img